Wednesday, 19 December 2012

6~ Capacitor With a Dielectric

$C= \frac{\varepsilon A}{d}$

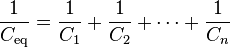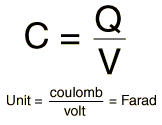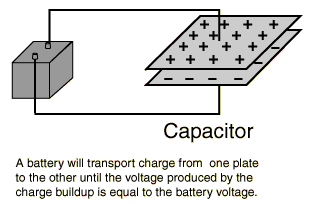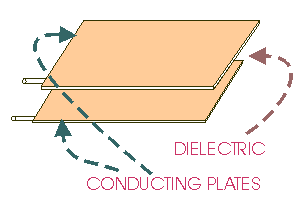
A capacitor

is composed of two conductors separated by

an insulating material called a DIELECTRIC. The dielectric can be paper, plastic film,

ceramic, air or a vacuum.

The plates can be aluminium discs, aluminium foil or a thin film of metal applied to

opposite sides of a solid dielectric.

The CONDUCTOR - DIELECTRIC - CONDUCTOR sandwich

can be rolled into a cylinder or left flat.

Happy Watching !

Do enjoy this video :)

p/s : Do not forget to make your own notes during watching this lesson.

Capacitance of simple systems

Calculating the capacitance of a system amounts to solving the Laplace equation ∇²φ=0 with a constant potential φ on the surface of the conductors. This is trivial in cases with high symmetry. There is no solution in terms of elementary functions in more complicated cases.

For quasi-two-dimensional situations analytic functions may be used to map different geometries to each other. See also Schwarz-Christoffel mapping.

Capacitance of simple systems
Type	Capacitance	Comment
Parallel-plate capacitor	$\varepsilon A /d$	ε: Permittivity
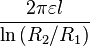
Coaxial cable	$\frac{2\pi \varepsilon l}{\ln \left( R_{2}/R_{1}\right) }$	ε: Permittivity
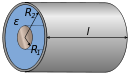
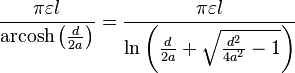
Pair of parallel wires	$\frac{\pi \varepsilon l}{\operatorname{arcosh}\left( \frac{d}{2a}\right) }=\frac{\pi \varepsilon l}{\ln \left( \frac{d}{2a}+\sqrt{\frac{d^{2}}{4a^{2}}-1}\right) }$
Wire parallel to wall	$\frac{2\pi \varepsilon l}{\operatorname{arcosh}\left( \frac{d}{a}\right) }=\frac{2\pi \varepsilon l}{\ln \left( \frac{d}{a}+\sqrt{\frac{d^{2}}{a^{2}}-1}\right) }$	a: Wire radius d: Distance, d > a $l$ : Wire length
Two parallel coplanar strips	$\varepsilon l \frac{ K\left( \sqrt{1-k^{2}} \right) }{ K\left(k \right) }$	d: Distance w₁, w₂: Strip width k_i: d/(2w_i+d) k²: k₁k₂ K: Elliptic integral $l$ : Length
Concentric spheres	$\frac{4\pi \varepsilon}{\frac{1}{R_{1}}-\frac{1}{R_{2}}}$	ε: Permittivity
Two spheres, equal radius	$2\pi \varepsilon a\sum_{n=1}^{\infty }\frac{\sinh \left( \ln \left( D+\sqrt{D^{2}-1}\right) \right) }{\sinh \left( n\ln \left( D+\sqrt{ D^{2}-1}\right) \right) }$ $=2\pi \varepsilon a\left\{ 1+\frac{1}{2D}+\frac{1}{4D^{2}}+\frac{1}{8D^{3}}+\frac{1}{8D^{4}}+\frac{3}{32D^{5}}+O\left( \frac{1}{D^{6}}\right) \right\}$ $=2\pi \varepsilon a\left\{ \ln 2+\gamma -\frac{1}{2}\ln \left( \frac{d}{a}-2\right) +O\left( \frac{d}{a}-2\right) \right\}$	a: Radius d: Distance, d > 2a D = d/2a γ: Euler's constant
Sphere in front of wall	$4\pi \varepsilon a\sum_{n=1}^{\infty }\frac{\sinh \left( \ln \left( D+\sqrt{D^{2}-1}\right) \right) }{\sinh \left( n\ln \left( D+\sqrt{ D^{2}-1}\right) \right) }$	a: Radius d: Distance, d > a D = d/a
Sphere	$4\pi \varepsilon a$	a: Radius
Circular disc	$8\varepsilon a$	a: Radius
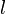Thin straight wire, finite length	$\frac{2\pi \varepsilon l}{\Lambda }\left\{ 1+\frac{1}{\Lambda }\left( 1-\ln 2\right) +\frac{1}{\Lambda ^{2}}\left[ 1+\left( 1-\ln 2\right) ^{2}-\frac{\pi ^{2}}{12}\right] +O\left(\frac{1}{\Lambda ^{3}}\right) \right\}$	a: Wire radius $l$ : Length Λ: ln( $l$ /a)

5~ Storing Energy in an Electrid Field

This is the list of formula regarding on this subtopic :

Uses of Capacitors

Capacitors are used for several purposes:

Timing - for example with a 555 timer IC controlling the charging and discharging.

Smoothing - for example in a power supply.

Coupling - for example between stages of an audio system and to connect a loudspeaker.

Filtering - for example in the tone control of an audio system.

Tuning - for example in a radio system.

Storing energy - for example in a camera flash circuit.

Factors Affecting Capacitance

How Capacitors Work

Have a look : Types Of Capacitor

A cylindrical capacitor is a

parallel plate capacitor that has been rolled up with an

insulating layer between the plates

4~ Capacitor in Series & Parallel

Capacitors in parallel

* have the same applied voltage

* their capacitance add up

* charge is apportioned among them by size

* using the schematic diagram to visualize parallel plates, it is apparent that each capacitor contributes to the total surface area.

$C_\mathrm{eq}= C_1 + C_2 + \cdots + C_n$

capacitors in parallel

Capacitors in series

* the capacitors each store instantaneous charge build-up equal to that of every other capacitor in the series

* the total voltage difference from end to end is apportioned to each capacitor according to the inverse of its capacitance

* the entire series acts as a capacitor smaller than any of its components.

$\frac{1}{C_\mathrm{eq}} = \frac{1}{C_1} + \frac{1}{C_2} + \cdots + \frac{1}{C_n}$

capacitors in series

NOTE : Capacitors are combined in series to achieve a higher working voltage, for example for smoothing a high voltage power supply.

LINK LINK LINK ...

this is the related link in this subtopic ..

http://www.technologystudent.com/elec1/capac1.htm

feel free to take a look :)

Here you go : KNOWLEDGE INPUT

Electrolytic capacitors are ‘polarised’ which means they have a positive and negative lead and must be positioned in a circuit the right way round (the positive lead must go to the positive side of the circuit).

They also have a much higher capacitance than non-electrolytic capacitors.

Non-electrolytic capacitors usually have a lower capacitance.

They are not polarised (do not have a positive and negative lead) and can be placed anyway round in a circuit.

They are normally used to smooth a current in a circuit.

CAPACITANCE - means the value of a capacitor.

3~ Calculating The Capacitance

A Parallel-Plate Capacitor

A Cylindrical Capacitor

A Spherical Capacitor

An Isolated Sphere

how to derive :

2~ Capacitance and capacitor

Capacitance is typified by a parallel plate arrangement and is defined in terms of charge storage:

1 farad = 1F = 1 coulomb per volt = 1 C/V

Capacitors

1~ What Is Capacitor?

CAPACITOR

Capacitors are components that are used to store an electrical charge and are used in timer circuits. A capacitor may be used with a resistor to produce a timer. Sometimes capacitors are used to smooth a current in a circuit as they can prevent false triggering of other components such as relays. When power is supplied to a circuit that includes a capacitor - the capacitor charges up. When power is turned off the capacitor discharges its electrical charge slowly.

tHE uSES OF capaCItoR :
* storing energy as potential energy in an electric field

Sunday, 16 December 2012

Let's Get It Started !!

Assalamualaikum...

hello everyone !

anhyeonghaseyo !

hye !

zhao shang hao !

apa khabar! :)

It's such a pleasure to write this blog about what we have learn during electric and magnet class for this semester. Thanks to our beloved lecturer Pn. Farrah Masyitah for giving us a task to build a blog about "Capacitor And Capacitance". Why we say that?? huhu.. Coz we are only an amateur before this to be happen (i mean before we do blog )........but frankly speaking, right this time we are exactly much better than before (in terms of doing blog *but only the simple one* ). plus we are getting more excited to learn electric and magnet subject.

So, before we proceed further, presenting our group members ....

DENG DEDEDEDEDEDENG.......

najla, radin and zyra

zyra and hajar